Imagine you’re a politician, and you want to redistribute from rich to poor so that poor people can afford housing. There are broadly two ways you could do this. First, you could tax the rich and spend the money on housing, either through cash transfers or housing vouchers, or by buying homes and renting them at below-market rates. This would be ideal, but raising taxes is politically unpopular. Second, you could require housing developers to provide subsidized homes as a condition for approving their new construction projects, a policy known as “inclusionary zoning” (IZ). For example, an IZ policy may require a developer to rent 20% of the homes in their new apartment building at 50% of average market rents. IZ has no public budgetary cost, and hence is appealing to politicians. But of course, there is a cost to pay: IZ is directly a tax on developers, which makes marginal projects infeasible, thereby reducing housing supply and increasing home prices; so it’s also indirectly a tax on new housing. To evaluate whether IZ is a good policy, we need to compare the benefits of subsidized homes against the costs of this ‘IZ tax’.
Instead of forcing developers to provide subsidized homes with no compensation (known as unfunded IZ), a better approach is to give them something in exchange (funded IZ). This ‘payment’ to developers could be a property tax exemption, reduced parking requirements, permit fast-tracking, or a density bonus (allowing more homes than under the current zoning). We say an IZ policy is calibrated when the value of the payment is at least equal to the cost of the subsidized homes, to avoid imposing a tax on new housing. The first three examples represent a pure cost: we have to give up tax revenue, reduce street parking spaces per resident, and delay permits for other projects. These forms of payment are economically equivalent to raising taxes and paying the developer in cash.
But a density bonus is special. When zoning is suboptimal and constrains development, new density creates surplus land value that we can use to fund redistribution. Since apartments are more lucrative than a single house, upzoning increases the option value of a parcel, raising its land value. Density-bonus IZ, when properly calibrated, funds the new subsidized homes using this surplus land value.1 Separately, the new market-rate housing is a benefit in itself. The more market housing we have, the more we reduce market-rate prices (through vacancy chains); this allows more people to find housing in the market, thereby reducing the need for subsidized housing in the first place.2 More density makes it easier to achieve our redistributive goal, because market-rate housing is complementary to below-market housing.3
In contrast, when IZ is funded by a property tax exemption (with no density bonus), we have to give up tax revenue to get subsidized homes. But when we allow more density, we actually benefit from higher market-rate supply and lower prices (and more property tax revenue). Housing is a benefit, not a cost. It would be one thing if we had to increase market-rate prices in order to get subsidized homes. But through density bonuses we can get both: lower market-rate prices and more subsidized housing (funded by surplus land value). There’s no tradeoff, relative to the baseline of suboptimal restrictive zoning.
If density-bonus IZ can create subsidized housing out of nothing, then what is the optimal number of IZ projects? Suppose you’re a politician who cares only about the amount of subsidized housing. In this case, you should max out on IZ apartment buildings to maximize the number of subsidized homes.4 If you instead use density bonuses sporadically (instead of systematically covering the region with IZ apartments), that’s like finding a pile of hundred dollar bills on the sidewalk and picking up only one or two.5 In practice, we don’t see any cities engaged in IZ-maxxing. This suggests that local governments are not in fact subsidized-housing maximizers, and are willing to trade off a substantial number of subsidized homes to protect neighborhood character or to avoid higher infrastructure costs.
If upzoning via density-bonus IZ creates a surplus, why not just do pure upzoning? Because new density raises land values, and in principle, this land value can be captured for public benefit. The simplest method is using a land value tax, but properly-calibrated IZ achieves the same goal. To capture all of the surplus, we have to keep upzoning until we reach the optimal zoning, where zoning regulations are not a binding constraint on development. So IZ is a transitionary policy, to be used only as we move to the optimal zoning. Cities that use IZ as a way to prevent further upzoning are undermining overall welfare.6 Again, IZ is funded out of surplus land value, and uncalibrated IZ is harmful because it imposes a tax on new housing.7 If politicians are unable to commit to a calibrated IZ policy, it may be best to avoid using it altogether.
Varieties of inclusionary zoning
There are many different ways to implement IZ.8 The main factors are the share of subsidized homes and the level of rent reduction. An IZ policy that requires 20% of units to rent at 50% of market rents means the developer gets 90% of the rental income of a market-rate building (80% of units at 100% market rents + 20% of units at 50% market rents), on top of administrative costs like verifying tenant incomes. IZ can be voluntary or mandatory, and unfunded or funded. It may apply at a threshold in building size, such as apartments with 20 units.9 Developers can provide subsidized homes on- or off-site10, or may make an in-lieu cash payment instead of providing in-kind subsidized homes. This variation in policy details makes it difficult to study IZ using panel regressions, since the average effect across such different programs is uninformative.
Soltas (2024) (published, working paper) studies a voluntary property tax exemption IZ program in New York City. He estimates a marginal cost of $1.6M per subsidized unit, driven by developer participation in expensive neighborhoods like Manhattan. This suggests evaluating IZ using a cash benchmark: is the program better than simply buying homes and renting them out at subsidized rates? In this case, the program seems poorly targeted by geography. Of course homes in Manhattan will be more expensive than in the Bronx!
Krimmel and Wang (2024) (published, working paper) studies a mandatory density-bonus IZ program in Seattle. They find that developers avoided the upzoned policy region and chose to build in other neighborhoods. This implies the program was not calibrated: the IZ tax on developers was larger than the payment (of higher density), so developers declined to participate. Similarly, Kestelman (2025) (working paper) shows that a voluntary density-bonus IZ program in Los Angeles did not increase the housing stock relative to neighboring areas. Again, comparing to a cash benchmark is helpful: if your bid for a home is below the market price, of course the seller will reject your offer.
Evidence from structural and simulation models
Rollet (2025) (working paper) builds a parcel-level general equilibrium model of housing supply and demand in New York City. The model accounts for the costs of redeveloping existing buildings, with redevelopment more likely to occur where prices are high and density is low. Using the estimated model, Rollet performs a policy experiment to evaluate the effects of IZ. The baseline scenario simulates NYC’s growth until 2060, assuming 13% growth in housing floorspace and 8% population growth, and holding zoning fixed at 2019 levels. The IZ policy is mandatory and unfunded, and requires 20% of floorspace to be rented at 50% of market-rate rents.
Rollet finds that floorspace increases by 13% in the baseline scenario. Under IZ, floorspace decreases by 1% relative to the baseline. So IZ reduces housing supply, because the IZ tax makes some projects infeasible.11 This implies an increase in market-rate rents (not shown in the current draft), which in turn increases the need for subsidized housing. The ‘exchange rate’ is 1.6 square feet of market-rate housing lost for each square foot of below-market-rate housing gained.12 Rollet doesn’t report the effect of IZ on aggregate welfare, but it is possibly welfare-reducing, because the cost of higher market rents outweigh the benefits of new subsidized homes.13
Rollet also considers a transit-oriented upzoning policy, where density is increased to FAR=6 within 0.25 miles of a transit station and to FAR=4 within 0.5 miles; this is a 59% increase in allowed density citywide. Upzoning increases built floorspace by 16% over the baseline. Combining upzoning and IZ produces a relative increase of 12%, again demonstrating how the IZ tax reduces supply. In this case, the density bonus from upzoning allows more projects to be feasible, but total supply is still lower than under pure upzoning. Again, we want to see the welfare analysis here, since we need to compare the benefit of more subsidized homes against the cost of fewer market-rate homes and higher market rents.
Lebret et al. (2025) (working paper) also builds a parcel-level model of housing in New York City, but using housing units instead of floorspace. They compare upzoning and unfunded mandatory IZ policies to a baseline after ten years. The IZ policy requires 30% of units to be rented at 50% of market rents (so landlords get 85% of rental income). Similar to Rollet (2025), they find that IZ adds subsidized units at the cost of losing market-rate units, and reduces total supply on net (see their Fig. 5A). The IZ policy has an exchange rate of 1.2 market-rate units lost for each subsidized unit gained.14
The upzoning policy increases allowed density by 25% uniformly across the city. Upzoning increases market-rate supply by 36% compared to baseline.15 A combined upzoning + IZ policy leads to a relative increase in total supply of 27%, driven by a reduction in market-rate supply and an even-larger increase in subsidized units.16 So as with Rollet, they find that the total number of housing units is lower under IZ + upzoning than under pure upzoning. But the count of total units is not the final story, since we care about aggregate welfare.
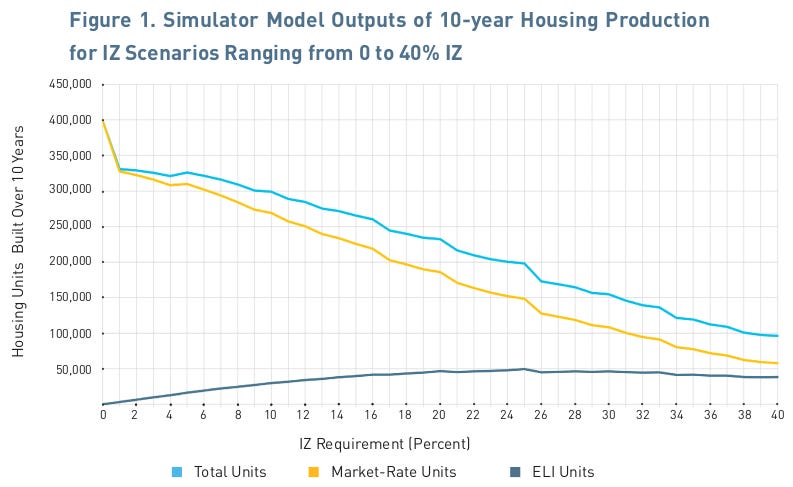
Phillips (2024) (published) studies IZ using simulations of Los Angeles’ Transit Oriented Communities (TOC) program, which is a voluntary density-bonus IZ policy adopted in 2017. The TOC program allows higher density near transit stops, as well as other incentives like reduced parking requirements. TOC has four tiers, with the fourth tier providing the largest density bonus of 55% higher residential FAR. The IZ requirement varies, but in practice involves developers renting homes to extremely-low-income (ELI) households, defined as 30% of area median income. The fourth tier has an IZ requirement of 11% of units rented to ELI households.
Phillips uses the Terner Housing Policy Simulator to compare the effects of different IZ requirements. The Simulator first assigns an optimal housing type to each parcel, and then applies a real estate pro forma to determine the probability of development over ten years. We can calculate the effect of a policy on the expected number of homes by multiplying the probability of development by the number of homes for each parcel, and aggregating across parcels.
The main results are reported in Phillips’ Figure 1, shown below. Higher IZ requirements (ELI units per building) consistently reduce market-rate supply (yellow line), while having an inverted-U relationship with subsidized ELI homes. The negative effect of IZ on market-rate units indicates that the IZ tax outweighs the density bonus, making projects infeasible even at low IZ requirements.17 Hence, the TOC density bonus is miscalibrated, and does not provide enough funding to developers to compensate for the IZ tax.
The ELI units follow a Laffer curve, with maximum ELI production of roughly 50,000 units at 25% IZ. At higher IZ requirements, we get fewer subsidized ELI homes, because so many projects are made infeasible by the IZ tax. Note that IZ has diminishing returns: requiring 16% IZ translates to only 7800 fewer ELI units compared to 25% IZ. More importantly, the cost of IZ is dramatic: at 25% IZ, the exchange rate is 5.1 market-rate units lost for each ELI unit gained. This exchange rate is minimized at 16% IZ, at 4.3 market-rate units lost per ELI unit.
Phillips does not explicitly model the effect of lower market-rate supply on rents. Instead, he calculates the increase in market rents needed to cancel out the monetary subsidy to ELI units. For example, at 16% IZ, the rent discount on ELI units is $1.41B. Since 85% of renters pay market rents, the loss in housing supply need only cause a small increase in rents to raise aggregate market rental costs by $1.41B. Specifically, the 16% IZ policy has zero financial benefits if the reduction in supply increases rents annually by 0.8% (over a 4% baseline).18 This shows how easily an IZ policy can be self-defeating.
Phillips shows that 16% IZ + TOC produces more total housing than a no-IZ, no-upzoning scenario (260k vs 245k units). But this is still less than a no-IZ upzoning scenario (400k). To identify the optimal policy, we need a model capable of doing welfare analysis, since the utility benefits of subsidized homes are plausibly larger than the benefits of market-rate homes. It is possible that pure upzoning maximizes aggregate social welfare, by reducing market-rate rents and the need for subsidized housing.
Other issues
IZ means the government is delegating the task of providing subsidized housing to private developers. On the face of it, this outsourcing of the welfare state is odd and likely suboptimal. Developers do not have a comparative advantage in implementing social policy, and may even abuse their power, for example, allocating subsidized homes as a form of compensation to their junior employees. Cook et al. (2025) (working paper) develops a model where subsidized homes are rationed by private developers; they find a small effect of developers favoring higher-income applicants. Moreover, IZ creates barriers to entry, favoring large-scale developers who can navigate the bureaucracy. Allowing in-lieu cash payments helps smaller developers avoid costly and time-consuming negotiations. A simpler approach would use a land value tax to fund nonprofit-run subsidized housing.
Unfunded IZ funds subsidized housing through a narrow tax base: developers and (via higher housing prices) purchasers of new market-rate housing. This is not optimal from a tax theory perspective. Moreover, if subsidized housing is a social good, benefitting the entire community, then it should be funded by the community as a whole. In contrast, density-bonus IZ pays for the subsidized homes out of the land value surplus created by upzoning, rather than by taxing developers and new residents.
One misconception about miscalibrated IZ is that the market-rate homes in an IZ apartment building cross-subsidize the non-market homes. But developers cannot set above-market rents, because renters would simply find cheaper rents elsewhere. Instead, it is the market-rate homes across the entire city that do the cross-subsidizing. In other words, the pass-through of the IZ tax is market-wide rather than at the building level. A miscalibrated IZ policy (where the IZ tax exceeds the payment to developers) raises rents market-wide, by killing marginal projects and reducing supply. In practice, developers in a growing city can wait for rents to rise so that the IZ policy becomes calibrated; but note that this is equivalent to IZ causing higher rents.
Density-bonus IZ creates a surplus because zoning is suboptimal and a binding constraint on development. So as we upzone and reduce the scarcity of apartment-zoned land, the magnitude of the surplus decreases. Hence, the number of subsidized homes we can fund per upzoned parcel decreases as the city becomes fully upzoned. Note that this is a sign of success: under the optimal zoning, upzoning creates no land value surplus. Moreover, the benefit is captured through lower housing prices, which allows more people to afford market-rate housing.
An open question is how well local governments can calibrate the IZ tax and developer payment, to avoid reducing supply and raising prices. In principle, cities can capture the upzoning surplus during the transition to the optimal zoning. This becomes more complicated when we consider a dynamic model, where developers anticipate future upzonings and delay construction while waiting for IZ requirements to be reduced (to maintain calibration at a smaller surplus). Political economy factors also matter, for example, with cities having perverse incentives to downzone so their IZ policy has more leverage. A land value tax would avoid such problems.
Specifically, developers pay for the subsidized homes by reducing their bid for the land, so the landowner sees little to no increase in land value. Hence, IZ is paid for by landowners, not developers. Note that we could also fund subsidized housing directly by capturing the surplus land value using a land value tax.
Similarly, Corinth and Irvine (2023) (published, working paper) shows how lower market-rate rents allow more people to access housing vouchers, because each dollar of the voucher budget buys more housing.
Does it make economic sense for a city to downzone so that upzoning creates a land value surplus? No. Downzoning reduces the land value of the affected parcels, so any subsequent density bonus merely raises land values back to the starting point; no value is created. In contrast, new density creates new value. This downzone-then-upzone strategy is just a transfer from landowners to the government.
In technical terms, a social planner with an objective function equal to the number of subsidized homes faces an optimization problem with a corner solution: maximize the number of IZ buildings. For example, in Vancouver the Broadway Plan allows high-rise IZ apartment buildings with 20% of units at below-market rents. So every 130-unit building produces 26 subsidized homes, and we maximize this number by allowing Nmax IZ projects and producing 26*Nmax subsidized homes, where Nmax is the total number of parcels in the city.
If the new housing supply reduces market rents and makes additional buildings unfeasible, then the IZ requirements can be reduced as well (e.g., from 20% to 10% subsidized homes).
Berkeley’s first IZ policy was passed to block new housing. IZ proponents “understood that no private, speculative developer would either desire to provide lower class housing, or be able to afford such inclusion without subsidies.”
In general, value capture policies need to be carefully calibrated to account for geographic differences and changing market conditions. The lack of such calibration separately by parcel is a worrying problem.
Aside: inclusionary zoning is not the opposite of exclusionary zoning. The latter uses single-family zoning to exclude poor people by banning cheaper types of housing. Anti-exclusionary zoning is just zoning that allows apartment buildings.
Why not apply IZ to all buildings, including single-family homes? From a value capture perspective, no surplus is created unless we allow higher density through upzoning. Since single-family homes maintain the status quo density, there’s no extra land value to capture. However, this misses the increases in land value that are driven by increased demand, and cannot be captured by policies (like IZ) that apply only conditional on redevelopment. So IZ is an incomplete value capture policy. In contrast, a land value tax would capture land value increases from single-family homes, because it applies unconditionally. And note that this is focusing only on land value; higher density has further benefits from increased housing supply and property taxes.
One justification for IZ is income mixing, to allow people with different incomes to live in the same neighborhood. Allowing off-site subsidized homes does not achieve this goal.
This effect seems small for an unfunded IZ policy with no density bonus (since the zoning is held fixed at 2019 levels). One possible explanation is that 2019 zoning is not binding, and contains enough bonus density for most developers to absorb the IZ tax.
Rollet reports that IZ increases floorspace by 147M for below-market-rate and -89M in total, so the market-rate change is -89 -147 = -236, and the exchange rate per below-market-rate sqft is 236/147 = 1.6.
Accounting for diminishing marginal utility would help IZ, for the standard reason that below-market homes go to poorer people with higher marginal utility.
Table 5 shows that IZ (Policy 3) produces -61,828 market-rate units and +51,075 subsidized units.
Supply increases by 193,587 units under baseline, and by an additional 70,298 under upzoning.
Net additional supply is 52,686 units = -27,247 market-rate + 79,394 subsidized.
Note that the IZ policy rounds up when converting from percentages to units, so the effective IZ requirement is higher than the nominal requirement. For example, a 1% nominal requirement on a 3-unit building means providing one below-market unit, or a 33% effective IZ requirement. This explains the sharp drop in market-rate units from 0 to 1% IZ. It is possible that the density bonus outweighs the IZ tax at low effective requirements, with the market-rate line being flat for some effective IZ levels before decreasing.
And note that this doesn’t include the beneficial effects of higher supply in LA on neighboring regions.
There are always trade offs. There is no free lunch. There is always an opportunity cost for what could have been done in absence of IZ. It’s even illustrated in the chart of units by IZ rate. The unit maximizing rate of IZ is 0%.
IZ is failing in Seattle and the requirement is vanishingly small, a few handful % of the project value.
Ultimately, when you’re in a housing deficit, IZ is just choosing favorites about who gets displaced. When the market is in disequilibrium because of a shortage, there will be a loser, IZ just says it’s someone who doesn’t/can’t fill out the paperwork.
Whoa, comment avvidentally posted when trying to edit!
Was trying to say that in the real world the way Congress appropriates, and HUD allocates, voucher funding results in PHAs having to attrit vouchers—not use cost savings to expand the number of people served. In any event, landlord discrimination against voucher users, as well as racial groups, is still a real barrier to raising voucher utilization and lease up rates, even in jurisdictions that have Source of Income laws.
There is also a common misconception that maximizing market rate housing is the goal and adding a market rate unit is inherently more beneficial than building a subsidized unit. Almost always economic models are cited as support. But these models and studies are unduly narrow in how they measure costs & benefits—usually the aggregate rent saving in tiny amounts across a market of hundreds of thousands of people. Rarely do they make an attempt to measure and consider non-monetary QoL and economic mobility benefits, much less the benefits of desegregation, when IZ enables a lower income family to access the resources and growth in the strong, affluent areas where most new development takes place. And the subsidy pays for itself over time in higher productivity (and lower social costs) as adults of children who grow up in those areas This is a glaring omission in light of the work of other economists like Raj Chetty. My non-scientific opinion is that one unit with deep subsidy in a well resourced area has more overall social value than 3 or 4 high end market rate units.
Then there is the infatuation with filtering, an easy out of difficult moral tradeoffs. For a number of reasons filtering does not inevitably add decent quality housing supply affordable to the poor and is not a substitute for subsidies. The <30% AMI poor are not even in the mainstream market. They live in a shadow market doubled up, on the street, in abandominiums or substandard housing. In high demand areas units are as likely to filter up, as well as down. In low demand areas units fall out of the bottom of the market and become abandoned. Those that do filter down to the poor are often not fit for habitation. But this is real world, out of sight from most of us.
Most disingenuous is the argument that IZ is a type of tax and it would be more efficient and equitable to use tax dollars to provide subsidized housing. As though that is likely to happen in the real world of austerity budgets and GOP rule at federal and state level and NIMBY opposition on the local level. As if there are other sites in strong neighborhoods where Affordable Housing projects are likely to get approved and built. More funding from tax revenues would be great! But instead of the benefits of desegregation and better economic mobility, health and education outcomes, that approach is likely to yield continued economic and/or racial segregation.